Τάβλι και πιθανότητες.
Posted on 9th Aug 2019 Leave a Comment
Το τάβλι είναι ένα παιχνίδι που χρησιμοποιεί τη χρήση δύο πρότυπων ζαριών. Κατά τη διάρκεια μιας στροφής στο τάβλι, ένας παίκτης μπορεί να μετακινήσει τα πούλια του σύμφωνα με τους αριθμούς που εμφανίζονται στα ζάρια.
Οι αριθμοί που δείχνουν τα ζάρια μπορούν να χωριστούν μεταξύ των δύο πούλιων, ή μπορούν να αθροιστούν και να χρησιμοποιηθούν για ένα μόνο πούλι. Για παράδειγμα, όταν ένας παίκτης τύχει 4 και 5 , ο παίκτης έχει δύο επιλογές: μπορεί να μετακινήσει το ένα πούλι τέσσερα κενά και το άλλο πέντε, ή ένα πούλι μπορεί να μετακινηθεί συνολικά σε εννέα κενά.
Για να διατυπώσουμε στρατηγικές στο τάβλι είναι χρήσιμο να γνωρίζουμε κάποιες βασικές πιθανότητες. Δεδομένου ότι ένας παίκτης μπορεί να χρησιμοποιήσει ένα ή δύο ζάρια για να μετακινήσει ένα συγκεκριμένο πούλι, οποιοσδήποτε υπολογισμός των πιθανοτήτων θα το λάβει αυτό υπόψη.
Για τις πιθανότητες του τάβλι μας, θα απαντήσουμε στην ερώτηση: “Όταν ρίχνουμε δύο ζάρια, ποια είναι η πιθανότητα να κυλήσουμε τον αριθμό n είτε ως ένα σύνολο δύο ζαριών είτε σε τουλάχιστον ένα από τα δύο ζάρια;”
Υπάρχουν συνολικά έξι αποτελέσματα, που αντιστοιχούν σε καθέναν από τους ακέραιους αριθμούς από το 1 έως το 6. Έτσι, κάθε αριθμός έχει πιθανότητα 1/6 να συμβεί.
Όταν ρίχνουμε δύο ζάρια, κάθε ζάρι είναι ανεξάρτητο από το άλλο. Εάν παρακολουθούμε τη σειρά του αριθμού που εμφανίζεται σε κάθε ζάρι, τότε υπάρχουν συνολικά 6 x 6 = 36 εξίσου πιθανά αποτελέσματα. Έτσι, ο 36 είναι ο παρονομαστής για όλες μας τις πιθανότητες και κάθε συγκεκριμένο αποτέλεσμα των δύο ζαριών έχει πιθανότητα 1/36.
Η πιθανότητα να κυλήσει σε έναν αριθμό
Η πιθανότητα να κυλήσει δύο ζάρια και να πάρει τουλάχιστον ένα από έναν αριθμό από το 1 έως το 6 είναι εύκολο να υπολογιστεί. Αν θέλουμε να καθορίσουμε την πιθανότητα να τύχουμε τουλάχιστον ένα 2 με δύο ζάρια, πρέπει να γνωρίζουμε πόσα από τα 36 πιθανά αποτελέσματα περιλαμβάνουν τουλάχιστον ένα 2. Οι τρόποι να γίνει αυτό είναι:
(2, 2), (2, 2), (3, 2), (4, 2), (5,2) , 4), (2, 5), (2, 6)
Έτσι, υπάρχουν 11 τρόποι να τύχετε τουλάχιστον ένα 2 με δύο ζάρια και η πιθανότητα να τύχετε τουλάχιστον ένα 2 με δύο ζάρια είναι 11/36.
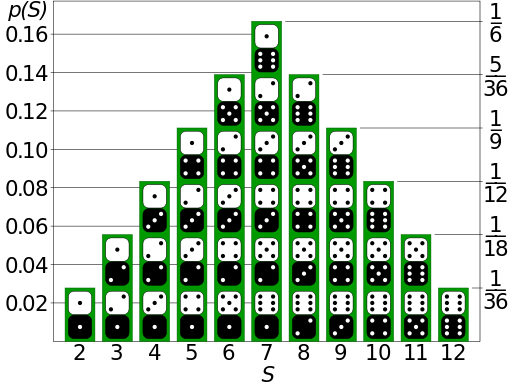
Πιθανότητα για ένα συγκεκριμένο άθροισμα
Οποιοσδήποτε αριθμός από δύο έως δώδεκα μπορεί να ληφθεί ως το άθροισμα των δύο ζαριών. Οι πιθανότητες για δύο ζάρια είναι λίγο πιο δύσκολο να υπολογιστούν. Δεδομένου ότι υπάρχουν διάφοροι τρόποι για να φτάσετε αυτά τα ποσά, δεν αποτελούν ενιαίο χώρο δείγματος. Για παράδειγμα, υπάρχουν τρεις τρόποι να κυλήσουμε ένα άθροισμα τεσσάρων: (1, 3), (2, 2), (3, 1), αλλά μόνο δύο τρόποι να κυλήσουμε ένα άθροισμα 11: (5, 6) 6, 5).
Η πιθανότητα να κυλήσει ένα άθροισμα ενός συγκεκριμένου αριθμού έχει ως εξής:
Η πιθανότητα να κυλήσει ένα άθροισμα των δύο είναι 1/36.
Η πιθανότητα να κυλήσει ένα άθροισμα τριών είναι 2/36.
Η πιθανότητα να κυλήσει ένα άθροισμα των τεσσάρων είναι 3/36.
Η πιθανότητα να κυλήσει ένα άθροισμα των πέντε είναι 4/36.
Η πιθανότητα να κυλήσει ένα άθροισμα των έξι είναι 5/36.
Η πιθανότητα κύλισης ενός ποσού επτά είναι 6/36.
Η πιθανότητα κυλίσεως ενός οκτώ είναι 5/36.
Η πιθανότητα κυλίσεως ενός εννέα είναι 4/36.
Η πιθανότητα να κυλήσει ένα σύνολο δέκα είναι 3/36.
Η πιθανότητα κυλίσεως ενός έντεκα είναι 2/36.
Η πιθανότητα να κυλήσει ένα άθροισμα των δώδεκα είναι 1/36.

Τελικά έχουμε όλα όσα χρειαζόμαστε για να υπολογίσουμε τις πιθανότητες για τάβλι. Καλή τύχη!
11 ψηφιακά εργαλεία εκπαίδευσης για εκπαιδευτικούς και μαθητές.
Posted on 9th Aug 2019 Leave a Comment
Εκατοντάδες εργαλεία ψηφιακής εκπαίδευσης έχουν δημιουργηθεί με σκοπό να δοθεί αυτονομία στον μαθητή, να βελτιωθεί η διαχείριση των ακαδημαϊκών διαδικασιών, να ενθαρρυνθεί η συνεργασία και να διευκολυνθεί η επικοινωνία μεταξύ εκπαιδευτικών και εκπαιδευομένων.
Εδώ παρουσιάζουμε 11 από τα πιο δημοφιλή.
1. Edmodo

Η Edmodo είναι μια εκπαιδευτική τεχνολογική εταιρεία που προσφέρει μια πλατφόρμα επικοινωνίας, συνεργασίας και προγύμνασης σε σχολεία και καθηγητές υποχρεωτικής εκπαίδευσης. Το δίκτυο Edmodo επιτρέπει στους καθηγητές να μοιράζονται περιεχόμενο, να διανέμουν κουίζ, να αναθέτουν και να διαχειρίζονται την επικοινωνία με τους μαθητές, τους συναδέλφους και τους γονείς. Το Edmodo είναι πολύ εκπαιδευτικό στο επίκεντρο του σχεδιασμού και της φιλοσοφίας του: οι μαθητές και οι γονείς μπορούν να συμμετάσχουν στην Edmodo μόνο αν τους ζητηθεί από έναν δάσκαλο. Οι δάσκαλοι και οι μαθητές δαπανούν μεγάλο χρονικό διάστημα στην πλατφόρμα, τόσο μέσα όσο και έξω από την τάξη.
2. Socrative
Το Socrative είναι ένα διαδικτυακό εργαλείο αξιολόγησης των μαθητών που επιτρέπει στους εκπαιδευτικούς να δημιουργούν κουίζ και άλλες εκπαιδευτικές ασκήσεις για την τάξη τους καθώς και να παρακολουθούν τις απαντήσεις τους σε πραγματικό χρόνο.
3. Projeqt
Το Projeqt είναι ένα εργαλείο που σας επιτρέπει να δημιουργείτε παρουσιάσεις πολυμέσων, με δυναμικές διαφάνειες, στις οποίες μπορείτε να ενσωματώσετε διαδραστικούς χάρτες, συνδέσμους, online κουίζ, χρονοδιαγράμματα Twitter και βίντεο, μεταξύ άλλων επιλογών. Κατά τη διάρκεια μιας διδασκαλίας στην τάξη, οι εκπαιδευτικοί μπορούν να μοιράζονται με φοιτητές ακαδημαϊκές παρουσιάσεις προσαρμοσμένες οπτικά σε διαφορετικές συσκευές.
4. Thinglink

Το Thinglink επιτρέπει στους εκπαιδευτικούς να δημιουργούν διαδραστικές εικόνες με μουσική, ήχους, κείμενα και φωτογραφίες. Αυτά μπορούν να μοιραστούν σε άλλους ιστότοπους ή σε κοινωνικά δίκτυα, όπως το Twitter και το Facebook. Το Thinglink προσφέρει τη δυνατότητα στους εκπαιδευτικούς να δημιουργήσουν μεθοδολογίες μάθησης που αφυπνίζουν την περιέργεια των μαθητών μέσω διαδραστικού περιεχομένου που μπορεί να επεκτείνει τις γνώσεις τους.
5. TED-Ed

Το TED-Ed είναι μια εκπαιδευτική πλατφόρμα που επιτρέπει τη δημιουργία εκπαιδευτικών μαθημάτων με τη συνεργασία καθηγητών, φοιτητών, εμψυχωτών – γενικά ανθρώπων που θέλουν να επεκτείνουν τη γνώση και τις καλές ιδέες. Αυτός ο ιστότοπος επιτρέπει τον εκδημοκρατισμό της πρόσβασης σε πληροφορίες, τόσο για τους εκπαιδευτικούς όσο και για τους φοιτητές. Εδώ, οι άνθρωποι μπορούν να συμμετέχουν ενεργά στη διαδικασία μάθησης των άλλων.
6. Padlet

Το Padlet είναι ένα διαδικτυακό εργαλείο που επιτρέπει στους εκπαιδευτικούς και τους μαθητές να συλλέγουν πληροφορίες από το διαδίκτυο και να τις αναρτούν πάνω στον ψηφιακό πίνακα ανακοινώσεων με τη μέθοδο «σύρε και τοποθέτησε» (drag and drop). Βίντεο, κείμενα, υπερσύνδεσμοι, εικόνες μπορούν να προστεθούν στον πίνακα ανακοινώσεων και να οργανωθούν, όπως ακριβώς θα οργανωνόταν και ένας κανονικός πίνακας ανακοινώσεων γεμάτος ανακοινώσεις. Οι μαθητές/χρήστες μπορούν ακόμη να «αναρτήσουν» αρχεία που έχουν δημιουργήσει, όπως σημειώσεις μαθημάτων ή εργασίες. Η εφαρμογή επιτρέπει την κοινή χρήση ενός πίνακα από περισσότερα άτομα, δίνοντας έτσι τη δυνατότητα για ομαδοσυνεργατικές εργασίες ή projects.
7. ClassDojo

Το ClassDojo είναι ένα εργαλείο για τη βελτίωση της συμπεριφοράς των μαθητών: οι καθηγητές παρέχουν στους μαθητές τους άμεση ανατροφοδότηση, έτσι ώστε η καλή διάθεση στην τάξη να «ανταμείβεται» με σημεία και οι μαθητές έχουν μια πιο δεκτική στάση απέναντι στη μαθησιακή διαδικασία. Το ClassDojo παρέχει ειδοποιήσεις σε πραγματικό χρόνο στους σπουδαστές, όπως το “Well Done David!” και “+1”, για συνεργασία. Οι πληροφορίες που συλλέγονται σχετικά με τη συμπεριφορά των μαθητών μπορούν να μοιραστούν αργότερα με τους γονείς και τους διαχειριστές μέσω του ιστού.
8. eduClipper

Αυτή η πλατφόρμα επιτρέπει στους εκπαιδευτικούς και τους μαθητές να μοιράζονται και να διερευνούν αναφορές και εκπαιδευτικό υλικό. Στο eduClipper, μπορείτε να συλλέξετε πληροφορίες που βρίσκονται στο Διαδίκτυο και στη συνέχεια να τις μοιραστείτε με τα μέλη των ομάδων που δημιουργήσατε προηγουμένως, η οποία προσφέρει τη δυνατότητα αποτελεσματικότερης διαχείρισης του ακαδημαϊκού περιεχομένου που βρίσκεται online, τη βελτίωση των ερευνητικών τεχνικών και την ψηφιακή καταγραφή των επιτευγμάτων κατά τη διάρκεια του μαθήματος. Παρομοίως, παρέχει την ευκαιρία στους εκπαιδευτικούς να οργανώσουν μια εικονική τάξη με τους μαθητές τους και να δημιουργήσουν ένα χαρτοφυλάκιο όπου αποθηκεύεται όλη η εργασία που πραγματοποιείται.
9. Storybird

Το Storybird στοχεύει στην προώθηση της γραφής και της ανάγνωσης δεξιοτήτων στους μαθητές μέσω της αφήγησης. Σε αυτό το εργαλείο, οι εκπαιδευτικοί μπορούν να δημιουργήσουν διαδραστικά και καλλιτεχνικά βιβλία στο διαδίκτυο μέσω ενός απλού και εύχρηστου περιβάλλοντος εργασίας. Οι ιστορίες που δημιουργούνται μπορούν να ενσωματωθούν σε ιστολόγια, να σταλούν μέσω ηλεκτρονικού ταχυδρομείου και να εκτυπωθούν, μεταξύ άλλων επιλογών. Στο Storybird, οι εκπαιδευτικοί μπορούν επίσης να δημιουργήσουν προγράμματα με τους μαθητές, να δώσουν συνεχή ανατροφοδότηση και να οργανώσουν μαθήματα και βαθμούς.
10. Animoto

Το Animoto είναι ένα ψηφιακό εργαλείο που σας επιτρέπει να δημιουργείτε βίντεο υψηλής ποιότητας σε σύντομο χρονικό διάστημα και από οποιαδήποτε κινητή συσκευή, εμπνέοντας τους μαθητές και συμβάλλοντας στη βελτίωση των ακαδημαϊκών μαθημάτων. Η διασύνδεση Animoto είναι φιλική και πρακτική, επιτρέποντας στους εκπαιδευτικούς να δημιουργούν οπτικοακουστικό περιεχόμενο προσαρμοσμένο στις εκπαιδευτικές ανάγκες.
11. Kahoot!

Kahoot! είναι μια εκπαιδευτική πλατφόρμα που βασίζεται σε παιχνίδια και ερωτήσεις. Μέσω αυτού του εργαλείου, οι εκπαιδευτικοί μπορούν να δημιουργήσουν ερωτηματολόγια, συζητήσεις ή έρευνες που συμπληρώνουν τα ακαδημαϊκά μαθήματα. Το υλικό προβάλλεται στην τάξη και οι ερωτήσεις απαντώνται από τους μαθητές ενώ παίζουν και μαθαίνουν ταυτόχρονα. Kahoot! προωθεί τη μάθηση βάσει παιχνιδιών, η οποία αυξάνει την εμπλοκή των μαθητών και δημιουργεί ένα δυναμικό, κοινωνικό και διασκεδαστικό εκπαιδευτικό περιβάλλον.
Ο Κώδικας Fibonacci -Tο αριθμητικό σύστημα της φύσης
Posted on 8th Aug 2019 Leave a Comment
Ο Κώδικάς Fibonacci
Ο κώδικας αυτός αποτελείται απλώς από μια σειρά αριθμών. Η σειρά αυτή δεν έχει τίποτα το ιδιαίτερο ή περίεργο. Οι εφαρμογές της όμως έχουν κάνει τον …γύρω του “κόσμου”, αφού όπως είδατε επεκτείνονται σε γη και ουρανό – ακόμη και ύδωρ (υδάτινους πόρους της γήινης επικράτειας).
Οι Αριθμοί της Σειράς Fibonacci λοιπόν έχουν ως εξής…
Ξεκινούν από το 0 και το 1 (τι πιο απλό!).
Από κει και πέρα όλοι οι επόμενοι βρίσκονται (υπολογίζονται) από το Άθροισμα των 2 προηγούμενων.
Έτσι η Σειρά Fibonacci αποτελείται από τους εξής Αριθμούς:
0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, κ.ο.κ.
Η Σειρά Fibonacci δεν κάνει …στάση (δεν σταματάει) πουθενά. Προχωράει συνεχώς μέχρι να φτάσει στο (Μαθηματικό) Άπειρο. Επιπλέον, ο λόγος δύο διαδοχικών αριθμών της ακολουθίας Φιμπονάτσι τείνει προς την χρυσή τομή ή χρυσή αναλογία, δηλαδή τον αριθμό φ=1,618033989.
Όπως οι περισσότερες Σειρές που ανεβαίνουν προς τα πάνω.Αυτό που μας ενδιαφέρει τώρα είναι …
Η Σχέση του Κώδικα Fibonacci με τον Αριθμό “φ” (1,618…)
Η σχέση αυτή ορίζεται Μαθηματικά ως εξής:
- Παίρνουμε ένα ζεύγος δύο Διαδοχικών Αριθμών από την Σειρά Fibonacci, από τον 13ο και μετά, π.χ. 377 και 233
- Υπολογίζουμε το Πηλίκο των 2 αυτών αριθμών και έχουμε τον Αριθμό …”φ”.
- Π.χ. 377 / 233 = 1,618
Κάντε το κι εσείς! Όσο μεγαλύτερα Διαδοχικά ζεύγη αριθμών χρησιμοποιείτε, τόσο πιο ακριβές είναι το πηλίκο, το οποίο πλησιάζει τον Αριθμό “φ” όλο και περισσότερο, δηλαδή με περισσότερα δεκαδικά ψηφία.
Υπέροχοι και μυστήριοι χαρακτηρίζονται αυτοί οι αριθμοί και απαντώνται παντού και σε διάφορες επιστήμες. Εκπληκτικός όμως είναι ο τρόπος με τον οποίο οι αριθμοί Φιμπονάτσι εμφανίζονται στη φύση.
Είναι το αριθμητικό σύστημα της φύσης. Τους συναντάς παντού, στη διάταξη των φύλλων ενός φυτού, στο μοτίβο των πετάλων ενός λουλουδιού, στο άνθος της αγκινάρας, σε ένα κουκουνάρι ή στο φλοιό ενός ανανά. Ισχύουν για την ανάπτυξη κάθε ζωντανού οργανισμού, ενός κυττάρου, ενός κόκκου σιταριού, μιας κυψέλης μελισσών, ακόμη και για όλη την ανθρωπότητα.

Φωτογραφία raywillis
Τα φυτά δε γνωρίζουν για την ακολουθία Fibonacci – απλά μεγαλώνουν με τον πιο αποτελεσματικό τρόπο. Αν μετρήσει κανείς τα πέταλα ενός λουλουδιού, θα διαπιστώσει ότι ο αριθμός τους είναι συχνά 3, 5, 8, 13, 21, 34 ή ακόμα και 55. Σπάνια θα συναντήσουμε λουλούδι με δύο πέταλα. Υπάρχουν εκατοντάδες είδη, τόσο άγρια όσο και καλλιεργημένα με πέντε πέταλα. Τα λουλούδια με οκτώ πέταλα δεν είναι τόσο κοινά όπως με τα πέντε, αλλά υπάρχουν αρκετά γνωστά είδη. Λουλούδια με δέκα τρία, είκοσι ένα και τριάντα τέσσερα πέταλα είναι επίσης αρκετά κοινά.

Φωτογραφία knitalatte11
Μπορούμε να μετρήσουμε στις μαργαρίτες 13, 21, 34, 55, ή και 89 πέταλα. Οι κοινές μαργαρίτες του αγρού έχουν συνήθως 34 πέταλα γεγονός που σίγουρα επηρεάζει το αποτέλεσμα του παιχνιδιού «μ’ αγαπά δεν μ’ αγαπά». Ο κρίνος έχει τρία πέταλα, η νεραγκούλα έχει πέντε, κ.λ.π.

Φωτογραφία Panterka
Οι σπόροι του ηλίανθου κατανέμονται κυκλικά. Η σπείρα είναι προς τα έξω ενώ έχει διπλή κατεύθυνση, δηλαδή και όπως κινούνται οι δείκτες του ρολογιού και αντίστροφα από το κέντρο του λουλουδιού. Ο αριθμός των σπειρών στο κάθε φυτό δεν είναι ίδιος. Γιατί γενικά είναι είτε 21 και 34, είτε 34 και 55, είτε 55 και 89, ή 89 και 144; Ο αριθμός των σπειρών ενός ηλίανθου και προς τις δύο κατευθύνσεις είναι δύο διαδοχικοί αριθμοί στην ακολουθία Fibonacci.

Φωτογραφία lucapost
Όλα τα κουκουνάρια αναπτύσσονται σε σπείρες, ξεκινώντας από τη βάση όπου ήταν ο μίσχος, και πηγαίνοντας κυκλικά μέχρι να φτάσουμε στην κορυφή.

Φωτογραφία JJ Harrison
Η ακολουθία Φιμπονάτσι εμφανίζεται στις βελόνες αρκετών ειδών έλατου, τα φύλλα της λεύκας, της κερασιάς, της μηλιάς, της δαμασκηνιάς, της βελανιδιάς και της φιλύρας, στη διάταξη των πετάλων της μαργαρίτας και του ηλιοτρόπιου. Τη βλέπουμε στην επιφάνεια των κορμών των κωνοφόρων δέντρων και στους δακτύλιους των κορμών των φοικικόδεντρων.
Φωτογραφία RDBury
Στη φωτογραφία παραπάνω βλέπετε ένα μικρό χαμομήλι. Τα πέταλα που βρίσκονται στο κέντρο του λουλουδιού σχηματίζουν σπείρες, σύμφωνα με τη ακολουθία Φιμπονάτσι. Υπάρχουν 21 πιο σκούρες μπλε σπείρες και 13 σπείρες με τυρκουάζ χρώμα. Το 13 και το 21 είναι διαδοχικοί αριθμοί στην ακολουθία Fibonacci. Το κέλυφος των σαλιγκαριών ακολουθεί και αυτό την ακολουθία Fibonacci. Το ίδιο και το κέλυφος του ναυτίλου (μαλάκιο). Η μόνη διαφορά μεταξύ των δύο είναι ότι το κέλυφος του ναυτίλου αναπτύσσεται σε τρισδιάστατες σπείρες, ενώ το κέλυφος των σαλιγκαριών αναπτύσσεται σε δισδιάστατες σπείρες.

Φωτογραφία OpenCage

Φωτογραφία Chris 73 Η ακολουθία εφαρμόζεται στο σώμα του δελφινιού, στον αστερία και στο ανθρώπινο σώμα. Η αναλογία του μήκους του πήχη του χεριού προς το μήκος του χεριού ισούται με 1.618, δηλαδή ισούται με τη Χρυσή Αναλογία. Η αναλογία μεταξύ του μήκους και του φάρδους του προσώπου και η αναλογία του μήκους του στόματος προς το φάρδος της μύτης είναι μερικά ακόμα παραδείγματα της εφαρμογής των αριθμών αυτών στο ανθρώπινο σώμα.
Σίγουρα, αυτός ο συνδυασμός φύσης και μαθηματικών δεν είναι τυχαίος!! Άραγε, τα μαθηματικά αντιγράφουν τη φύση ή η φύση τα μαθηματικά;; Δεν συμφωνείτε όμως μαζί μου ότι είναι εκπληκτικός ο τρόπος που συνδυάζονται, όπως και το αποτέλεσμα;;

Φωτογραφία werner boehm

Φωτογραφία J Brew

Φωτογραφία daaynos

Φωτογραφία Just chaos

Φωτογραφία Oakwood30

Φωτογραφία paul mccoubrie

Φωτογραφία Rahmat_Isnaini

Φωτογραφία Ramesh NG

Φωτογραφία Grizdave

Φωτογραφία Grizdave

Φωτογραφία Grizdave

Φωτογραφία GOPAN G. NAIR

Φωτογραφία robinparmar
Σείριος | Το πιο λαμπρό αστέρι.
Posted on 3rd Aug 2019 Leave a Comment
Ποιο αστέρι είναι το πιο φωτεινό στον ουρανό μας;
Η απάντηση είναι ο Σείριος.
Ο Σείριος είναι το λαμπρότερο αστέρι στον νυχτερινό ουρανό. Βρίσκεται στον αστερισμό του Μεγάλου Κυνός. Το όνομά του προέρχεται από το ελληνικό “σείριος” που σημαίνει “φωτεινός”. Αν και με γυμνό οφθαλμό διακρίνεται ένα αστέρι, στην πραγματικότητα είναι διπλό άστρο. Βρίσκεται 8,6 έτη φωτός από την Γη.

Ο Σείριος είναι ορατός από σχεδόν όλη την Γη τους χειμερινούς μήνες (για το Βόρειο ημισφαίριο, εκτός αν ο παρατηρητής βρίσκεται βορειότερα από τις 73 μοίρες). Μαζί με τον Πρόκυνα και τον Μπετελγκέζ σχηματίζουν ένα φωτεινό τρίγωνο που έχει την ανεπίσημη ονομασία «Χειμερινό τρίγωνο».





